주성분분석 PCA
1. 입력 데이터의 공분산 행렬을 구한다.
2. 공분산 행렬을 고유값 분해해서 고유벡터와 고윳값을 구한다.
3. 고윳값이 가장 큰 K개의 고유벡터를 추출한다.
4. 고윳값이 가장 큰 순으로 추출된 고유벡터를 이용해 입력데이터들을 선형변환 (내적)
고유벡터, 고윳값
: 벡터가 회전하지 않고 확대나 축소만 할때 변화한 벡터의 길이 비율이 고윳값이 되며 그때의 벡터 방향이 고유벡터가 된다.
따라서 고유벡터는 행렬이 작용하는 주측의 방향을 나타내므로 공분산 행렬의 고유벡터는 데이터가 어떤 방향으로 분산되어 있는지를 나타내준다.

[실습] 고윳값 분해 알아보기
x = [[177.7, 68.1, 91.8], [168, 60.2, 89.3], [165.3, 49.1, 84.9], [159.1, 42, 86.3], [176.4, 73.3, 93.8],
[176, 57.2, 92.5], [170, 59.8, 89.8], [164.6, 51.6, 88.5], [174.4, 70.2, 91.7], [174.8, 58.8, 91.6]]
키 / 체중 / 가슴둘레 의 3가지 열로 구성되어있는 데이터가 존재한다.
[[177.7 68.1 91.8]
[168. 60.2 89.3]
[165.3 49.1 84.9]
[159.1 42. 86.3]
[176.4 73.3 93.8]
[176. 57.2 92.5]
[170. 59.8 89.8]
[164.6 51.6 88.5]
[174.4 70.2 91.7]
[174.8 58.8 91.6]]x = np.array(x)
print(x)
print('='* 30)
print('키 컬럼 분산:', np.round(np.var(x[:,0],ddof= 1),2)) # ddof : 자유도
print('='* 30)
print('열 평균:', np.mean(x, axis= 0))
print('='* 30)키 컬럼 분산: 38.75
==============================
열 평균: [170.63 59.03 90.02]키 컬럼에 관한 분산은 공분산행렬을 만든 후 비교하기 위함이다.
각 컬럼의 편차를 계산하기 위해 각 데이터의 열의 평균을 빼서 데이터를 원점을 중심으로 분포되도록 맞춰준다.
x = x - np.mean(x, axis= 0) # 각 컬럼의 편차 계산
print(x) # 표준화가 된 값 (평균이 영점으로 이동)
print('='* 30)
print('covariance(공분산행렬)')
cov = (x.T.dot(x))/ (len(x)-1)
print(cov)[[ 7.07 9.07 1.78]
[ -2.63 1.17 -0.72]
[ -5.33 -9.93 -5.12]
[-11.53 -17.03 -3.72]
[ 5.77 14.27 3.78]
[ 5.37 -1.83 2.48]
[ -0.63 0.77 -0.22]
[ -6.03 -7.43 -1.52]
[ 3.77 11.17 1.68]
[ 4.17 -0.23 1.58]]
==============================
covariance(공분산행렬)
[[38.749 52.035 15.779]
[52.035 95.54 23.158]
[15.779 23.158 7.984]]
공분산행렬을 구하는 식은

(여기서 x 는 원데이터의 평균을 제외한 값이다.)
(x.T.dot(x))/ (len(x)-1)을 진행하며 위와 같은 결과가 나온다.
COV 함수와 결과 비교하면
np.cov(x, rowvar= False ) # rowvar = True : 행이 특성값! 열이 관측값!array([[38.749, 52.035, 15.779],
[52.035, 95.54 , 23.158],
[15.779, 23.158, 7.984]])위에 직접 수식을 작성한 것과 같은 결과가 나오는 것을 알 수 있다.
고윳값, 고유벡터 행렬 구하기
고윳값과 고유벡터를 구해 튜플로 반환해준다.
eigenvalue, eigenvector = np.linalg.eig(cov)print('고윳값')
print(np.round(eigenvalue, 4)) # 가장 큰 순서부터 정렬되서 나옴고윳값
[132.696 8.307 1.27 ]
대각행렬이란 주대각선 상에 위치한 원소가 아닌 나머지가 0인 행렬을 말한다.
즉 고윳값 대각행렬이란 고윳값이 대각선으로 위치하고 나머지가 0인 행렬을 말한다.
print('고유값 대각행렬 (lambda)')
eig_matrix = np.identity(3) * eigenvalue # 정방 단위행렬 * 고윳값
print(eig_matrix)고유값 대각행렬 (lambda)
[[132.696 0. 0. ]
[ 0. 8.307 0. ]
[ 0. 0. 1.27 ]]
열에 대한 고유벡터는 n 번째 열에 대해 n 번째 고윳값을 가지고 만들어진 값이다.
print('고유벡터 행렬 (V)')
V = eigenvector
print(V) # 열벡터 = (1) 132.696 을 가지고 만들어낸 고유벡터고유벡터 행렬 (V)
[[-0.501 -0.803 -0.323]
[-0.838 0.544 -0.054]
[-0.219 -0.244 0.945]]
# 직교(내적 = 0)하는지
print('첫 번째 고유벡터와 두 번째 고유벡터와의 내적')
print(np.round(V[:,0].T.dot(V[:,1]),2))첫 번째 고유벡터와 두 번째 고유벡터와의 내적
0.0
print('공분산 행렬')
print(cov)공분산 행렬
[[38.749 52.035 15.779]
[52.035 95.54 23.158]
[15.779 23.158 7.984]]print('고윳값 분해를 통한 공분산 행렬 계산')
print(V @ eig_matrix @ np.linalg.inv(V)) # VλV-1고윳값 분해를 통한 공분산 행렬 계산
[[38.749 52.035 15.779]
[52.035 95.54 23.158]
[15.779 23.158 7.984]]값이 동일하게 나온다.
첫 번째 주성분 (PC1) 구하기
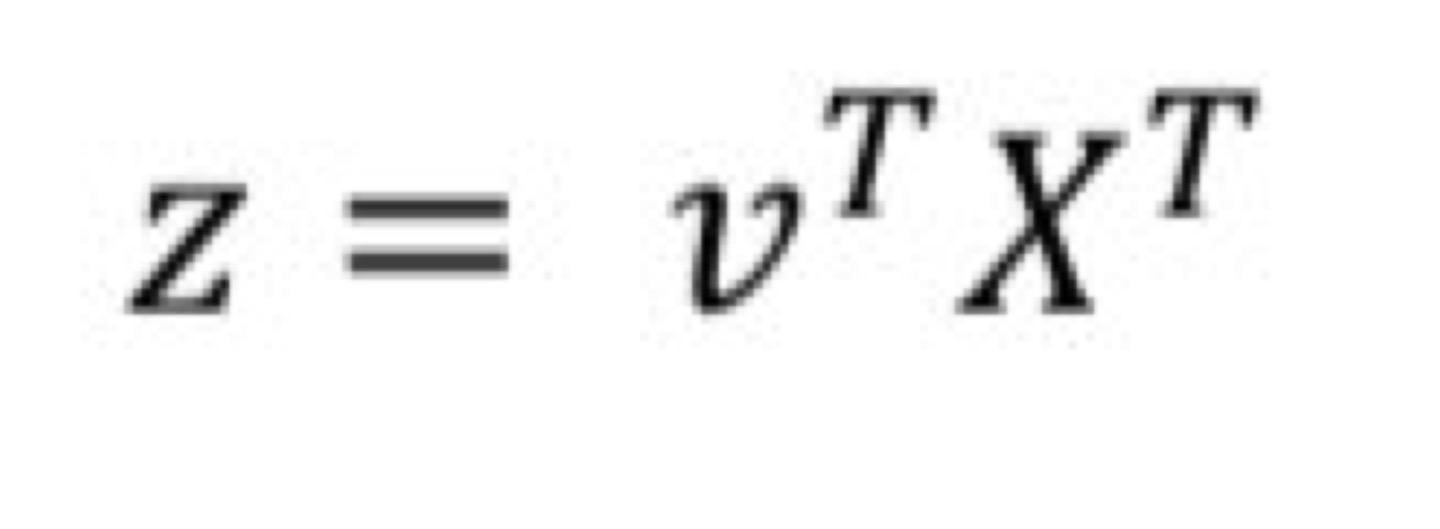
pc1 = V[:,0].T @ x.T
print(np.round(pc1,2))
# 분산이 가장 큰 축에서 직교시킨 점이 원점에서 얼마나 떨어져 있는지 나타내는 스칼라 값이다.[-11.53 0.49 12.11 20.85 -15.67 -1.7 -0.28 9.57 -11.61 -2.24]고유벡터를 가지고 첫 번째 주성분에 의해 만들어진 데이터이다.
해당 데이터는 분산이 가장 큰 축에서 직교시킨 점이 원점에서 얼마나 떨어져 있는지 나타내는 스칼라 값이다.
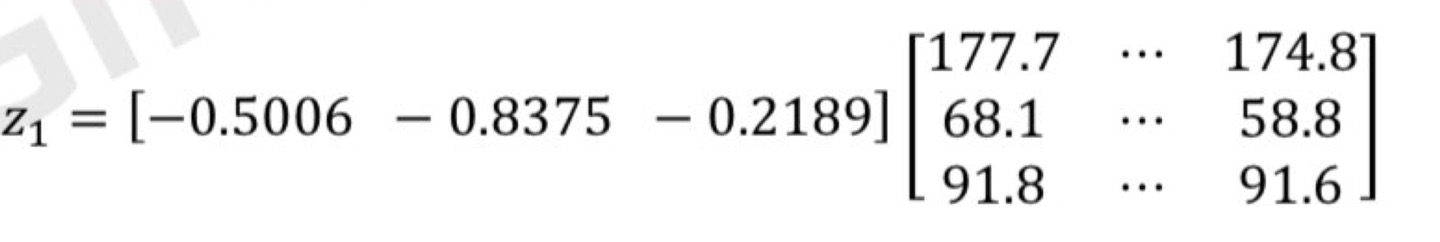
공분산을 이용한 주성분 분석
주성분분석 : 변수가 가지고 있는 정보의 손실을 최소화 하면서 변수의 차원을 축소하는 분석 기법이기 때문에 차원을 축소한다.
print('PCA를 이용한 차원 축소')
VT = np.array([ V[:,0], V[:,1]]) # 3차원 -> 2차원
print('고유벡터 VT - 주성분 2개 선택')
print(VT)PCA를 이용한 차원 축소
고유벡터 VT - 주성분 2개 선택
[[-0.501 -0.838 -0.219]
[-0.803 0.544 -0.244]]
print('고유벡터 VT 와 원 데이터 XT의 내적')
Z = VT @ x.T
print(Z.T)고유벡터 VT 와 원 데이터 XT의 내적
[[-11.526 -1.18 ]
[ 0.494 2.924]
[ 12.106 0.129]
[ 20.85 0.906]
[-15.668 2.204]
[ -1.699 -5.912]
[ -0.281 0.978]
[ 9.574 1.173]
[-11.61 2.637]
[ -2.241 -3.859]]
PCA 클래스와 결과 비교
from sklearn.decomposition import PCA
model = PCA(n_components= 2) # n_components : 몇 개의 주성분으로 압축할 것인가
pca = model.fit_transform(x)
print(pca) # 부호는 관계없음[[-11.526 1.18 ]
[ 0.494 -2.924]
[ 12.106 -0.129]
[ 20.85 -0.906]
[-15.668 -2.204]
[ -1.699 5.912]
[ -0.281 -0.978]
[ 9.574 -1.173]
[-11.61 -2.637]
[ -2.241 3.859]]
PC 가 차지하는 분산 비율
print(model.explained_variance_ratio_)
print(f'분산 합계 = {np.sum(model.explained_variance_ratio_):.2f}%')[0.933 0.058]
분산 합계 = 0.99%2차원으로 줄여도 분산의 합계가 유의미한 값인 것을 알 수 있다.
PCA를 통한 고유벡터와 고유값 확인
model.components_ # 차원 축소 할때 이용한 고유벡터 값array([[-0.501, -0.838, -0.219],
[ 0.803, -0.544, 0.244]])model.explained_variance_ # 차원 축소 할때 이용한 고윳값array([132.696, 8.307])
PCA 결과 지도학습에 적용하기 # 붓꽃 데이터
from sklearn.datasets import load_iris
import pandas as pdiris = load_iris()
df = pd.DataFrame(iris.data, columns= iris.feature_names)
display(df.head())lasses = iris.target
print(classes)
np.bincount(classes) # 빈도수 카운트[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]array([50, 50, 50], dtype=int64)
데이터 표준화
from sklearn.preprocessing import StandardScaler
iris_scaled = StandardScaler().fit_transform(iris.data)
주성분 분석
차원 축소 : 4차원 -> 2차원
from sklearn.decomposition import PCA
pca = PCA(n_components= 2)
iris_pca = pca.fit_transform(iris_scaled)
print(iris_pca.shape)(150, 2)
주성분 값 확인
df_iris_pca = pd.DataFrame(iris_pca, columns=(['PCA1','PCA2']))
df_iris_pca['class'] = iris.target
display(df_iris_pca.head())
2개 차원으로 데이터 시각화
import matplotlib.pyplot as plt
marker = ['o','s','^'] # 3가지 품종 따라 포인트를 다르게
for i, m in enumerate(marker):
x_data = df_iris_pca[df_iris_pca['class'] ==i]['PCA1']
y_data = df_iris_pca[df_iris_pca['class'] ==i]['PCA2']
plt.scatter(x_data,y_data, marker= m, label = iris.target_names[i]) # label = iris.target_names 실제품종의 이름을 가져옴
plt.legend()
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()
(비교) 꽃받침의 길이와 넓이로 데이터 시각화
df['class'] = iris.target
marker = ['o','s','^'] # 3가지 품종 따라 포인트를 다르게
for i, m in enumerate(marker):
x_data = df[df['class'] ==i]['sepal length (cm)']
y_data = df[df['class'] ==i]['sepal width (cm)']
plt.scatter(x_data,y_data, marker= m, label = iris.target_names[i]) # label = iris.target_names 실제품종의 이름을 가져옴
plt.l
PCA 에 따른 각 주성분이 차지하는 분산(설명력) 확인
print(f'분산 합계: {np.sum(pca.explained_variance_ratio_):.2f}%')분산 합계: 0.96%
적절한 차원 수 선택하기
pca = PCA() # 차원축소 되지 않고 주성분을 찾음
pca.fit(iris_scaled)
cumsum = np.cumsum(pca.explained_variance_ratio_)
# 누적 분산(설명력)이 0.95를 넘어서는 주성분의 개수
d = np.argmax(cumsum >= 0.95) + 1
print(d) # 임계값이 된다. 기준 이상이 되는누적 분산(설명력)이 0.95를 넘어서는 주성분의 개수를 찾기 위해 'np.argmax(cumsum >= 0.95) + 1' 을 한다.
주성분 수 계산을 위한 스크릿 플롯 그리기
plt.plot(np.arange(1,5),cumsum)
plt.axis([1,4,cumsum[0],1]) # 축 범위 지정
plt.plot([d,d], [0,cumsum[d-1]], 'k:') # (2,0) , (2,095).. 두 점을 잇는 선 그리기
plt.plot([1,d], [cumsum[d-1], cumsum[d-1]], 'k:') # (1,0.95...)(2, 0.95...) 두 점을 잇는 선 그리기
plt.plot(d,cumsum[d-1], 'ko')
plt.xlabel('Dimensions')
plt.ylabel('Explained Variance')
plt.grid(True)
plt.show()
최적의 주성분이 2차원으로 축소하는 것임을 알 수 있다.
PCA 성능비교 - 원본 데이터와 PCA가 적용된 데이터를 이용한 분류 알고리즘 적용 결과 비교
# PCA 없이
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
model1 = RandomForestClassifier(random_state=10)
score = cross_val_score(model1, iris_scaled, iris.target,cv = 3, scoring= 'accuracy')
print(f'교차검증 평균정확도: :{np.mean(score):.3f}')교차검증 평균정확도: :0.967# PCA로
model2 = RandomForestClassifier(random_state=10)
score = cross_val_score(model2, iris_pca, iris.target,cv = 3, scoring= 'accuracy')
print(f'교차검증 평균정확도: :{np.mean(score):.3f}')교차검증 평균정확도: :0.887
'풀스택 개발 학습 과정 > 머신러닝, 딥러닝' 카테고리의 다른 글
| [머신러닝] 추천 시스템 알고리즘 - 아이템 기반 최근접 이웃 필터링 (0) | 2024.08.01 |
|---|---|
| [머신러닝] 추천 시스템 알고리즘 - 콘텐츠 기반 필터링 (0) | 2024.08.01 |
| [머신러닝] 인공지능을 위한 수학(3. 선형대수) (0) | 2023.11.27 |
| [머신러닝] 비지도 학습 알고리즘 - 주성분분석(공분산행렬) - 1 (0) | 2023.11.26 |




