분류분석 Classification Analysis - 로지스틱 회귀분석
종속변수가 범주형인 데이터에 대해 데이터의 유사성이 높은 것들을 같은 종류로 분류 되도록 하는 분석방법
(종속변수가 미리 결정된 범주 중 하나에 속할 가능성 또는 확률을 예측(확률분포로 나타난다.))
종류
- 로지스틱 회귀분석: 종속변수가 범주형일때 사용하는 회귀분석 (이진분류에 많이 사용)
- 의사결정트리 : 나무 형태의 그래프로 의사결정을 표현하는 데이터 분류 알고리즘(시각화, 도식화 가능)
- 나이브 베이즈: 데이터 집합의 예측변수가 독립적이라고 가정하는 분류 알고리즘(조건부확률 사용)
- K-nearest Neighbors: 데이터 포인터 간의 거리를 기반으로 예측 분류 및 예측하는 알고리즘
로지스틱 회귀분석 Logistic Regression
일반 회귀분석 = 연속형 <> 로지스틱 회귀분석 = 범주형 사용
P(Y=1|X = x) : 입력값 X가 x일때, 출력값이 1일 확률
임계값으로 결정(디폴트 값은 0.5) : 임계값보다 클 경우 1, 작은 경우는 0으로 분류
일반 회귀분석의 종속변수 y는 실수이지만, 로지스틱 회귀분석은 0또는 1의 값을 갖기 때문에 선형 함수를 사용할 수 없다.
선형 함수를 사용할 경우 해당하는 값마다 기울기가 계속 변하게 되며 올바른 정답의 값이 달라지게 된다.
그러므로 로지스틱 회귀분석에서는 시그모이드 함수를 활용한 그래프를 그리게 된다.
(양수의 값이면 1에 수렴하고, 음수의 값은 0으로 수렴하는)

시그모이드 함수 그리기
mport numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1 + np.exp(-x))
# 1 + np.exp(-x) : 지수함수위의 로지스틱 모델인 p의 식을 함수로 만들어 놓는다.
x = np.arange(-5.0, 5.0, 0.1)
y = sigmoid(x)
plt.plot(x,y,'g')
plt.plot([0,0],[1.0,0.0],':') # 선 그리기
plt.title('Sigmoid Function')
plt.show()
# 양의 무한대 -> 1 / 음의 무한대 -> 0
# 선형회귀 모델을 이용해서 만들었기 때문에 w 값, b값을 구하는 것이 최종 목적
# 바꿔주면 경사도가 조금씩 변함
>> w의 값에 따라 경사도가 변한다(w = 선형회귀 모형에서 직선의 기울기를 의미한다)
3가지의 가중치를 받은 시그모이드 함수 만들어보기
x = np.arange(-5.0,5.0,0.1)
y1 = sigmoid(0.5 * x)
y2 = sigmoid(x) # 가중치 없는
y3 = sigmoid(2 * x)
plt.plot(x,y1,'r--', label = 'w:0.5') # w = 0.5
plt.plot(x,y2,'g', label = 'w:1') # w = 1
plt.plot(x,y3,'b--', label = 'w:2') # w = 2
plt.plot([0,0],[1.0,0.0],':') # 선 그리기
plt.title('Sigmoid Function')
plt.legend()
plt.show()
# 최적의 분류선을 찾아내는 것이 최종 목적
- 종속변수의 범위 [0, 1] 을 [∞,∞] 로 변경하기 위해 odds 활용
odds = 성공확률 / 실패확률 을 의미
- 로지스틱 회귀의 비용함수 또한 경사하강법을 이용하여 최적의 w(가중치)를 찾지만, 비용함수로 평균제곱오차를 사용하진 않는다. 이때 로지스틱 회귀에서 사용하는 비용함수를 크로스 엔트로피(Cross Entropy) 함수라고 한다.
이진분류의 경우 예측값과 정답값이 2개로 하나는 참(1) 이고, 하나는 거짓(0) 이다.
L = -(y-log(y_hat)) + (1-y)log(1-y_hat) [y: 타겟값, y_hat: 예측값]
| 타겟값 | 손실함수 | 추론값 |
| y = 1 | -log(y_hat) | y_hat = 1 일때 손실함수 값이 최소 (0) |
| y = 0 | -log(1-y_hat) | y_hat = 0 일때 손실함수 값이 최소(0) |
다항 로지스틱 회귀분석 Multiclass Logistic Regression
>> one-vs-one

구별 가능한 두 가지 클래스만 선택하여 회귀선을 그리게 된다.
(예시: 서포트 벡터 머신(학습데이터 크기에 민감한 알고리즘이다.))
>> one-vs-all(one-vs-rest)
회귀분석은 이진분류만 가능하기 때문에 모든 데이터를 사용하여 이진분류로 치환하는 또 다른 클래스를 만들어낸다.

각각을 분류해내는 회귀선이 총 3개가 존재하게 되며,
새로운 데이터를 넣게 되면 그 중 가장 높은 확률의 클래스로 속하게 된다.
분류모델의 평가지표
혼동행렬 Confusion Matrix
- 분류모델에서 알고리즘의 성능을 쉽게 시각화한 테이블 형태의 레이아웃을 말한다.
- 분류모델에 의해 분류예측이 실제와 같은지 다른지를 평가하는 방법이다.
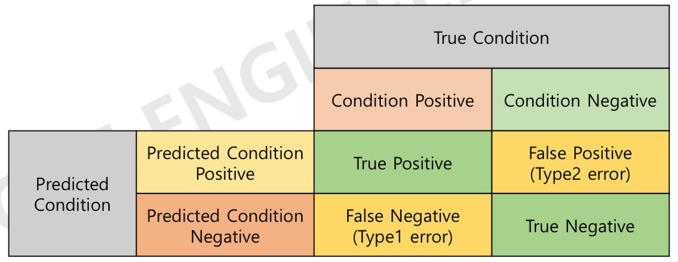
예측조건과 실제 조건은 행과 열이 바뀔 수 있다.
True / False : 실제와 비교했을때 // Positive/ Negative : 예측과 비교했을때 사용된다.
>> 정확도 accuracy : 전체 데이터 중 맞게 검출한 비율을 말한다.
accuracy = TP + TN / TP+ FP + FN + TN (즉, 전체 데이터를 더한 값에서 실제로 정답인 값을 가리킨다.)
불균형 데이터에서 정확도는 accuracy(정확도) 가 높다고 해도 좋은 모델이라고 할수 없다.
Positive를 맞출 확률도 있지만, Negative 를 맞출 확률도 높기 때문이다.
>> 재현율(민감도) recall : 실제 P를 P로 예측한 비율
recall = TP / TP + FN (즉, 실제로 일어날 모든 값에서 예측을 맞춘 값을 가리킨다.)
때문에 재현율이 높다는 것은 모델이 양성을 잘 찾아낸 다는 것을 뜻한다.
>> 특이도 specificity
specificity = TN / FP + TN (즉, 일어나지 않을 것이라 예측한 모든 값에서 일어나지 않은 값을 가리킨다.)
>> 정밀도 precision : P로 검출한 것 중 실제 P의 비율
precision = TP / TP + FP (즉, 정답을 예측한 것을 더한 값에서 실제로 예측을 맞춘값을 가리킨다. )
때문에 정밀도가 높다는 것은 모델이 예측한 것에 대해 신뢰도가 높다는 것을 뜻한다.
>> recall(재현율) - precision(정밀도) 관계
정밀도가 높다는 것은 모델이 신중하게 양성을 판단한다는 것을 가리키는데, 이때 신중한 양성 판단은 '양성판단을 잘 하지 않는다' 와 같은 의미를 가지게 된다. 그렇다면 즉 재현율이 올라갈 수 없다. 때문에 재현도와 정밀도는 turn - off의 관계가 되므로 함께 늘릴 수 없다.
>> (보완) F1 score : recall , precision 의 조화평균 값
F1 score = 2*P*R / P + R

Model1 의 accuracy 가 Model2의 accuracy 보다 낮지만, 종합적으로 보면 Model1이 더 좋은 모델임을 알 수 있다.
ROC / AUC
- ROC : 다양한 분류 임계값에서 참양성률과 거짓양성률이 이루는 곡선
- AUC : ROC curve 아래의 면적. AUC 가 높을수록 예측력이 높다.
AUC = 0.5 보다 아래라면 (즉, 대각선 아래면) 분류모델로서의 영향이 없는 것을 가리킨다.

'국비 교육 > 머신러닝, 딥러닝' 카테고리의 다른 글
| [머신러닝] 분류분석 : [다지분류]로지스틱 회귀분석 (0) | 2023.11.21 |
|---|---|
| [머신러닝] 분류분석 : [이지분류] 로지스틱 회귀분석 - (실습) 유방암 확률 예측, 개인 신용도 기반 대출 가능 여부 예측 (0) | 2023.11.21 |
| [머신러닝] 회귀분석 - 교차검증 (0) | 2023.11.20 |
| [머신러닝] 회귀분석 - L1, L2규제 ((문제) 보스톤 집값 예측, 대한민국 육군 몸무게 예측) (0) | 2023.11.20 |



